

Unlimited filter prototypes and automatic correction frequency bands.EQ Voicing (post target) using common filter prototypes.Automatic phase correction with smoothing.Automatic magnitude correction with smoothing.Phase Adjustment using minimum-phase and maximum-phase all-pass filters, and a unique 4th order all-pass parametric phase filter.Linear-phase complementary crossovers using common IIR low-pass and high-pass filter responses.Magnitude Adjustment using common filter prototypes, above, and with minimum, linear and maximum phase options.IIR reference mode and reference editor with IIR filter conversion between brands.General (all of the above filter types).IIR filter modes with brand-specific parameter limits.IIR coefficient export: regular transfer function and MiniDSP formats.Low-pass and high-pass Bessel, Butterworth, 2nd order variable Q, Chebyshev I & II, Elliptic, Linkwitz/Riley & Neville Thiele notched crossover.Direct FIR design, without a measurement.FIR filter design from a loudspeaker measurement.Continuous filter calculation and error display as parameters are updated.Intuitive, fast workflow from impulse response import through to filter coefficient export.
#Digital filter designer code
JavaScript code to calculate the impulse response of the ideal filter. The symmetry of the window function about the center point (j=Np) means that the window coefficients need only be calculated for 0 The methods used in this FIR generator were taken from the paper by J. The actually algorithm and the JavaScript code to implement it are presented at the bottom of the page.įIR Listing Kaiser-Bessel filter design formulae The filter coefficients are calculated and plotted along with a graph of the frequency response of the filter. Then press the "CALCULATE FILTER" button. To use it, set the sample rate (1kHz < Fs < 1MHz) and the type of filter desired low pass, band pass or high pass, then set the number of points in the filter (N < 500) then set the frequency of ideal filter edges (Fa, Fb) and the minimum attenuation (Att) required in the stop band. To demonstrate the power and simplicity of this technique, a Kaiser-Bessel filter generator is provided below. The Kaiser-Bessel window function is simple to calculate and its parameters can be adjusted to produce the desired maximum side lobe level for a near minimal filter length. This will increase the width of the transition region between the pass and stop bands but will lower the side lobe levels outside the pass band. To suppress the side lobes and make the filter frequency response approximate more closely to the ideal, the width of the window must be increased and the window function tapered down to zero at the ends. Rectangular windowing in the time domain will result in a frequency spectrum with the width of the pass band close to the desired value but with side lobes appearing at the band edges (the effects of time domain windowing on the frequency spectrum are discussed in more detail in the Spectrum Analyser page). The simplest window function is the rectangular window which corresponds to truncating the sequence after a certain number of terms. To create a Finite Impulse Response (FIR) filter, the time domain filter coefficients must be restricted in number by multiplying by a window function of a finite width. Unfortunately, the filter response would be infinitely long since it has to reproduce the infinitely steep discontinuities at the band edges in the ideal frequency response. The filter impulse response is obtained by taking the Discrete Fourier Transform (DFT) of the ideal frequency response. The basic idea behind the Window method of filter design is that the ideal frequency response of the filter is equal to 1 for all the pass band frequencies, and equal to 0 for all the stop band frequencies.#Digital filter designer generator
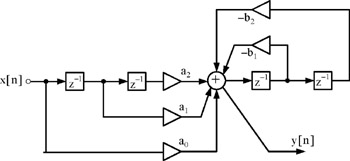


 0 kommentar(er)
0 kommentar(er)
